Get Started

Let’s develop a small language that allows for simple computation together. Here’s a valid input file for that language:

 
  puts(1 + 2)
  puts(4 + 2)

To install the parslet library, please do a

 
  gem install parslet

Now let’s write the first part of our parser. For now, we’ll just recognize simple numbers like ‘1’ or ‘42’.

 
  require 'parslet' 

  class Mini < Parslet::Parser
    rule(:integer) { match('[0-9]').repeat(1) }
    root(:integer)
  end

  Mini.new.parse("132432")  # => "132432"@0

Running this example will print “132432@0”. Congratulations! You just have written your first parser. Running it on the input ‘puts(1)’ will not work yet. Let’s see what happens in case of a failure:

 
  Mini.new.parse("puts(1)") # raises Parslet::ParseFailed

Here’s the error message provided by that exception: “Expected at least 1 of [0-9] at line 1 char 1.” parslet tries to find a number there, but can’t find one.

There are just two lines to the definition of this parser, let’s go through them:

 
  rule(:integer) { match('[0-9]').repeat(1) }

rule lets you create a new parser rule. Inside the block of that :integer rule, you find match('[0-9]').repeat(1). This says: “match a character that is in the range 0-9, then match any number of those, but at least match one.”

 
  root(:integer)

That second line just says: Start parsing at the rule called :integer.

Addition

Let’s go for simple addition. We’ll have to allow for spaces in our input, since those help make code readable.

 
  rule(:space)  { match('\s').repeat(1) }
  rule(:space?) { space.maybe }

Two things are new here: (and both in the second line)

you can use (‘call’) other rules in your rules
.maybe, the same as .repeat(0,1)¹, indicating that the thing before it is maybe present once in the input.

Essentially, you can think about parslet rules as instructing Ruby to “parse this” and “parse that”. Calling other rules can be looked at in the same way; you tell Ruby to go off, parse that subrule and then come back with the results. This helps when thinking about rule recursion. For example, a self-recursive rule like this one will of course create an endless loop:

 
  rule(:infinity) {
    infinity >> str(';')
  }

Even though infinity seems to be delimited by ‘;’, in reality, infinity is very long, especially towards the end. There is no way of knowing for the parser when to stop processing infinity and start reading semicolons. Ergo, we need to make sure we talk about concrete items that consume input first, and then do recursion. This way we ensure that our grammar terminates, since in a way, it is like a normal program.

Here’s the full parser:

  
  class Mini < Parslet::Parser
    rule(:integer)    { match('[0-9]').repeat(1) >> space? }
  
    rule(:space)      { match('\s').repeat(1) }
    rule(:space?)     { space.maybe }
  
    rule(:operator)   { match('[+]') >> space? }
  
    rule(:sum)        { integer >> operator >> expression }
    rule(:expression) { sum | integer }

    root :expression
  end

  def parse(str)
    mini = Mini.new
  
    mini.parse(str)
  rescue Parslet::ParseFailed => failure
    puts failure.parse_failure_cause.ascii_tree
  end

  parse "1 + 2 + 3"  # => "1 + 2 + 3"@0
  parse "a + 2"      # fails, see below

As you can see, the parser got decorated with the space? idiom. Every atom of our language consumes the space right after it. This is a useful convention that makes top level rules (the important ones) look cleaner.

Note also the addition of :operator, :sum and :expression. The runner code has been extended a bit, so as to throw nice explanations of what went wrong when a parse failure is encountered. Running the code on ‘a + 2’ for example outputs:

  
Expected one of [SUM, INTEGER] at line 1 char 1.
|- Failed to match sequence (INTEGER OPERATOR EXPRESSION) at line 1 char 1.
|  `- Failed to match sequence ([0-9]{1, } SPACE?) at line 1 char 1.
|     `- Expected at least 1 of [0-9] at line 1 char 1.
|        `- Failed to match [0-9] at line 1 char 1.
`- Failed to match sequence ([0-9]{1, } SPACE?) at line 1 char 1.
   `- Expected at least 1 of [0-9] at line 1 char 1.
      `- Failed to match [0-9] at line 1 char 1.

This is what parslet calls an #error_tree. Not only the output of your parser, but also its grammar is constructed like a tree. When things go wrong, every branch of the tree has its own reasons for not accepting a given input. The #parse_failure_cause method returns those reasons.

Our grammar has essentially two branches, SUM and INTEGER. Can you see why all rules expect a number as the first character?

Tree output (and what to do about it)

But if we leave the negative examples for a second; what happens if the parse succeeds? It turns out, not much:


  parse "1 + 2 + 3"  # => "1 + 2 + 3"@0

The only notable difference between input and output is that the output has an extra ‘@0’ appended to it. This is related to line number tracking and will be explained later on (or you can skip ahead and look up Parslet::Slice).

The code we now have parses the input successfully, but doesn’t do much else. Parslet hasn’t got its own opinion on what to do with your input. By default, it will just play it back to you. But parslet provides also a method of structuring its output:

 
  # Without structure: just strings.
  str('ooo').parse('ooo')                           # => "ooo"@0
  str('o').repeat.parse('ooo')                      # => "ooo"@0

  # Added structure: .as(...)
  str('ooo').as(:ex1).parse('ooo')                  # => {:ex1=>"ooo"@0}
  
  long = str('o').as(:ex2a).repeat.as(:ex2b).parse('ooo')  
  long # => {:ex2b=>[{:ex2a=>"o"@0}, {:ex2a=>"o"@1}, {:ex2a=>"o"@2}]}

You get to name things the way you want! This is also free. Seriously: parslet requires you to add all the structure to its output. Annotate important parts of your grammar with .as(:symbol) and get back a tree-like structure composed of hashes (sequence), arrays (repetition) and strings (like we had initially).

Once you start naming things, you’ll notice that what you don’t name, disappears. Parslet assumes that what you don’t name is unimportant.

 
parser =  str('a').as(:a) >> str(' ').maybe >> 
          str('+').as(:o) >> str(' ').maybe >> 
          str('b').as(:b)
parser.parse('a + b') # => {:a=>"a"@0, :o=>"+"@2, :b=>"b"@4}

Think of this like using a highlighter on your input: What is there not to like about neon yellow?

Making the parser complete

Let’s look at the complete parser definition that also allows for function calls:

 
class MiniP < Parslet::Parser
  # Single character rules
  rule(:lparen)     { str('(') >> space? }
  rule(:rparen)     { str(')') >> space? }
  rule(:comma)      { str(',') >> space? }

  rule(:space)      { match('\s').repeat(1) }
  rule(:space?)     { space.maybe }

  # Things
  rule(:integer)    { match('[0-9]').repeat(1).as(:int) >> space? }
  rule(:identifier) { match['a-z'].repeat(1) }
  rule(:operator)   { match('[+]') >> space? }
  
  # Grammar parts
  rule(:sum)        { integer.as(:left) >> operator.as(:op) >> expression.as(:right) }
  rule(:arglist)    { expression >> (comma >> expression).repeat }
  rule(:funcall)    { identifier.as(:funcall) >> lparen >> arglist.as(:arglist) >> rparen }
  
  rule(:expression) { funcall | sum | integer }
  root :expression
end

require 'pp'
pp MiniP.new.parse("puts(1 + 2 + 3, 45)")

That’s really all there is to it — our language is a really simple language. When fed with a string like ’puts(1 + 2 + 3, 45), our parser outputs the following:

 
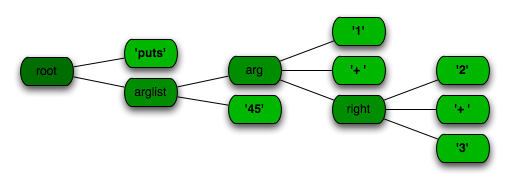
{:funcall=>"puts"@0,
 :arglist=>
  [{:left=>{:int=>"1"@5},
    :op=>"+ "@7,
    :right=>{:left=>{:int=>"2"@9}, :op=>"+ "@11, :right=>{:int=>"3"@13}}},
   {:int=>"45"@16}]}

Parslet calls this the intermediary tree. There are three types of nodes in this tree:

Hashes: a node that has named subtrees
Arrays: a node storing a collection of sub-nodes
Strings are the leaves, containing the accepted source

The format of this tree is easy to work with and to read. Here’s what the above tree would look like as a graphic:

Where to go from here: An Interpreter

As nice as the format above is for printing and looking at – it may be difficult at times to get the information out of it again. Let’s look at how to transform the tree:

 
class SimpleTransform < Parslet::Transform
  rule(funcall: 'puts', arglist: sequence(:args)) {
    "puts(#{args.inspect})"
  }
  # ... other rules
end

tree = {funcall: 'puts', arglist: [1,2,3]}
SimpleTransform.new.apply(tree) # => "puts([1, 2, 3])"

Transformation is an entire topic by itself; this will be covered in detail later on. To whet your appetite, let me just give you a few teasers:

Transformations match portions of your tree at any depth, replacing them with whatever you decide.
In addition to sequence(sym), there is also simple(sym) and subtree(sym). Those match simple strings and entire subtrees respectively. Caution with the latter.

Here’s how you would write a somewhat classical interpreter for our little language by using a transformation. Note that from this point on, there is not one way to go about this, but thousands; you are really free (and on your own):

 
class MiniP < Parslet::Parser
  # Single character rules
  rule(:lparen)     { str('(') >> space? }
  rule(:rparen)     { str(')') >> space? }
  rule(:comma)      { str(',') >> space? }

  rule(:space)      { match('\s').repeat(1) }
  rule(:space?)     { space.maybe }

  # Things
  rule(:integer)    { match('[0-9]').repeat(1).as(:int) >> space? }
  rule(:identifier) { match['a-z'].repeat(1) }
  rule(:operator)   { match('[+]') >> space? }
  
  # Grammar parts
  rule(:sum)        { 
    integer.as(:left) >> operator.as(:op) >> expression.as(:right) }
  rule(:arglist)    { expression >> (comma >> expression).repeat }
  rule(:funcall)    { 
    identifier.as(:funcall) >> lparen >> arglist.as(:arglist) >> rparen }
  
  rule(:expression) { funcall | sum | integer }
  root :expression
end

IntLit = Struct.new(:int) do
  def eval; int.to_i; end
end
Addition = Struct.new(:left, :right) do
  def eval; left.eval + right.eval; end
end
FunCall = Struct.new(:name, :args) do
  def eval; p args.map { |s| s.eval }; end
end

class MiniT < Parslet::Transform
  rule(:int => simple(:int))        { IntLit.new(int) }
  rule(
    :left => simple(:left), 
    :right => simple(:right), 
    :op => '+')                     { Addition.new(left, right) }
  rule(
    :funcall => 'puts', 
    :arglist => subtree(:arglist))  { FunCall.new('puts', arglist) }
end

parser = MiniP.new
transf = MiniT.new

ast = transf.apply(
  parser.parse(
    'puts(1,2,3, 4+5)'))
        
ast.eval # => [1, 2, 3, 9]

That’s a bunch of code for printing [1, 2, 3, 9]. Welcome to the fantastic world of compiler and interpreter writing!

¹ As far as parsing goes. There is a subtle difference between #repeat(0,1) and #maybe. Can you figure it out?